前言
从本篇开始我们将会一起来学习图相关的算法,图算有很多相当实用算法,比如:垃圾回收器的标记清除算法、地图上求路径的最短距离、拓扑排序等。在开始学习这些算法之前我们需要先来了解下图的基本定义,以及使用哪种数据结构来表示一张图,本篇我们先从无向图开始学习。
图的定义
图:是有一组顶点和一组能够将两个订单相连组成的。连接两个顶点的边没有方向,这种图称之为无向图。
图的术语
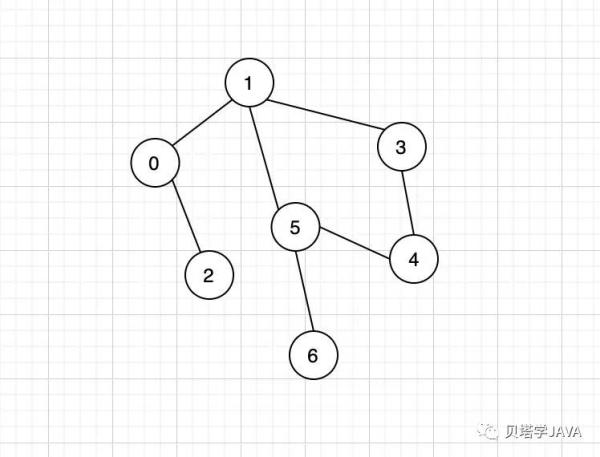
通过同一条边相连的两个顶点我们称这两个顶点相邻;
某个顶点的度数即表示连接这个顶点的边的总数;如上图:顶点1的度数是3
一条边连接了一个顶点与其自身,我们称为自环
连接同一对顶点的边称为平行边
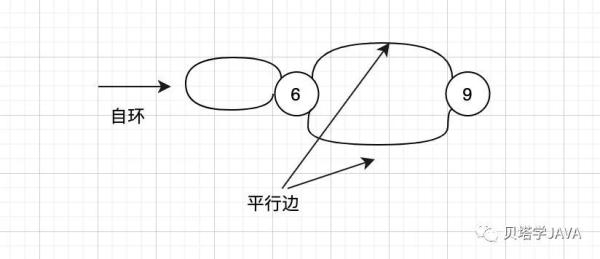
术语还有很多,暂时这里只列出本篇我们需要使用到的术语,后面有在使用到其他的术语再做解释,太多也不太容易记得住
如何表示出图
图用什么数据结构来表示主要参考两个要求:
在开发图的相关算法时,图的表示的数据结构是基础,所以这种数据结构效率的高 在实际的过程中图的大小不确定,可能会很大,所以需要预留出足够的空间
考虑了这两个要求之后大佬们提出以下三个方法来供选择:
邻接矩阵 键入有v个顶点的图,我们可以使用v乘以v的矩阵来表示,如果顶点v与w相连,那么把v行w列设置为true,这样就可以表示两个顶点相连,但是这个方式有个问题,如果遇到图很大,会造成空间的浪费。不满足第二点。其次这种方式没办法表示平行边 边的数组 可以定义一个表示的边对象,包含两个int属性表示顶点,但是如果需要找到某个顶点的相连顶点有哪些,我们就需要遍历一遍全部的边。这种数据结构的效率较差 邻接表数组 定义一个数组,数组的大小为顶点的个数,数据下标表示顶点,数组中每个元素都是一个链表对象(LinkedListQueue),链表中存放的值就是与该顶点相连的顶点。(LinkedListQueue我们已经在之前的文章中实现,可以参考文章《https://juejin.cn/post/6926685994347397127》)
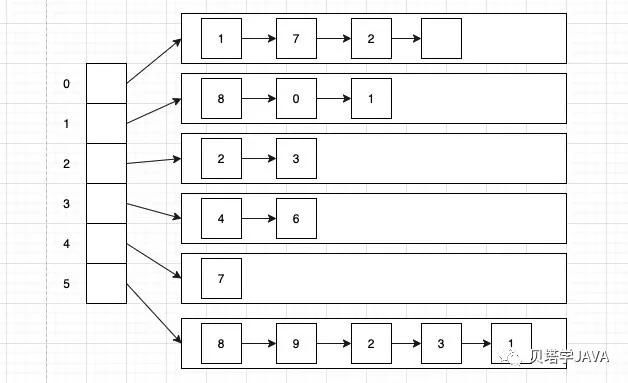
无向图的API定义 publicclassGraph{publicGraph(intV);//创建含有v个顶点不含边的图publicintV();//返回顶点的个数publicintE();//返回图中边的总数publicvoidaddEdge(intv,intw);//向图中添加一条边v-WpublicIterableadj(intv);//返回与v相邻的所有顶点publicStringtoString();//使用字符串打印出图的关系} 无向图API的实现
要实现上面定义的API,我们需要三个成员变量,v表示图中顶点的个数,e表示图总共边的数据,LinkedListQueue的数组用来存储顶点v的相邻节点;
构造函数会初始化空的邻接表数组
因为是无向图,所以addEdge方法在向图中添加边既要添加一条v->w的边,有需要添加一条w->v的边
publicclassGraph{privatefinalintv;privateinte;privateLinkedListQueue[]adj;publicGraph(intv){this.v=v;this.adj=(LinkedListQueue[])newLinkedListQueue[v];for(inti=0;i<v;i++){this.adj[i]=newLinkedListQueue<>();}}publicintV(){returnv;}publicintE(){returne;}publicvoidaddEdge(intv,intw){this.adj[v].enqueue(w);this.adj[w].enqueue(v);this.e++;}publicIterableadj(intv){returnthis.adj[v];}@OverridepublicStringtoString(){StringBuildersb=newStringBuilder();sb.append(v).append(\”个顶点,\”).append(e).append(\”条边 \”);for(inti=0;i<v;i++){sb.append(i).append(\”:\”);for(intj:this.adj[i]){sb.append(j).append(\”\”);}sb.append(\” \”);}returnsb.toString();}} 图的常用工具方法
基于图数据结构的实现,我们可以提供一些工具方法
计算顶点v的度数 顶点的度数就等于与之相连接顶点的个数
publicstaticintdegree(Graphgraph,intv){intdegree=0;for(intw:graph.adj(v)){degree++;}returndegree;}
计算所有顶点的最大度数
publicstaticintmaxDegree(Graphgraph){intmaxDegree=0;for(intv=0;v<graph.V();v++){intdegree=degree(graph,v);if(maxDegree<degree){maxDegree=degree;}}returnmaxDegree;}
计算所有顶点的平均度数 每条边都有两个顶点,所以图所有顶点的总度数是边的2倍
publicstaticdoubleavgDegree(Graphgraph){return2.0*graph.E()/graph.V();}
计算图中的自环个数 对于顶点v,如果v同时也出现了在v的邻接表中,那么表示v存在一个自环;由于是无向图,每条边都被记录了两次(如果不好理解可以把图的toString打印出来就可以理解了)
publicstaticintnumberOfSelfLoops(Graphgraph){intcount=0;for(intv=0;v<graph.V();v++){for(intw:graph.adj(v)){if(v==w){count++;}}}returncount/2;} 总结
本篇我们主要学习使用何种数据结构来表示一张图,以及基于这种数据结构实现了几个简单的工具方法,在下一篇我们将来学习图的第一个搜索算法 – 深度优先搜索
文中所有源码已放入到了github仓库:https://github.com/silently9527/JavaCore